Hur man bygger en invers matris. Matrix slough-lösning: Ett exempel på en lösning som använder en invers matris. Invers matrismetod

En invers matris för en given är en sådan matris, multiplikation av den ursprungliga med vilken ger en identitetsmatris: Ett obligatoriskt och tillräckligt villkor för närvaron av en invers matris är olikheten mellan determinanten för den ursprungliga (vilket i sin tur innebär att matrisen måste vara kvadratisk). Om determinanten för en matris är lika med noll, kallas den degenererad och en sådan matris har ingen invers. I högre matematik är inversa matriser viktiga och används för att lösa ett antal problem. Till exempel på hitta den inversa matrisen en matrismetod för att lösa ekvationssystem konstrueras. Vår servicesajt tillåter beräkna invers matris online två metoder: Gauss-Jordan-metoden och att använda matrisen av algebraiska additioner. Den första innebär ett stort antal elementära transformationer inom matrisen, den andra - beräkningen av determinanten och algebraiska tillägg till alla element. För att beräkna determinanten för en matris online kan du använda vår andra tjänst - Beräkna determinanten för en matris online

.

Hitta den omvända matrisen på webbplatsen

hemsida låter dig hitta invers matris online snabbt och gratis. På sajten görs beräkningar av vår tjänst och ett resultat visas med en detaljerad lösning för att hitta invers matris. Servern ger alltid bara det exakta och korrekta svaret. I uppgifter per definition invers matris online, är det nödvändigt att determinanten matriser var annorlunda än noll, annars hemsida kommer att rapportera omöjligheten att hitta den inversa matrisen på grund av att determinanten för den ursprungliga matrisen är lika med noll. Hitta uppgift invers matris finns i många grenar av matematiken, vilket är ett av de mest grundläggande begreppen inom algebra och ett matematiskt verktyg i tillämpade problem. Oberoende invers matrisdefinition kräver stor ansträngning, mycket tid, beräkningar och stor noggrannhet för att inte göra en halka eller ett litet fel i beräkningarna. Därför vår tjänst hitta den omvända matrisen online kommer att avsevärt underlätta din uppgift och kommer att bli ett oumbärligt verktyg för att lösa matematiska problem. Även om du hitta invers matris själv rekommenderar vi att du kontrollerar din lösning på vår server. Ange din ursprungliga matris på vår Beräkna invers matris online och kontrollera ditt svar. Vårt system är aldrig fel och hittar invers matris given dimension i läget uppkopplad omedelbart! På plats hemsida teckeninmatningar är tillåtna i element matriser, I detta fall invers matris online kommer att presenteras i allmän symbolisk form.

Detta ämne är ett av de mest hatade bland studenter. Ännu värre, förmodligen bara determinanter.

Tricket är att själva konceptet med det inversa elementet (och jag pratar inte bara om matriser nu) hänvisar oss till multiplikationsoperationen. Även i skolans läroplan anses multiplikation vara en komplex operation, och matrismultiplikation är i allmänhet ett separat ämne, som jag har ett helt stycke och en videolektion till det.

Idag kommer vi inte att gå in på detaljerna i matrisberäkningar. Kom bara ihåg: hur matriser betecknas, hur de multipliceras och vad som följer av detta.

Recension: Matrismultiplikation

Först av allt, låt oss komma överens om notation. En matris $A$ av storleken $\left[ m\times n \right]$ är helt enkelt en tabell med tal med exakt $m$ rader och $n$ kolumner:

\=\underbrace(\left[ \begin(matris) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ ((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n))) \\ ... & ... (1) & ...(m) & (m) & ((a)_(mn )) \\\end(matris) \right])_(n)\]

För att inte av misstag förväxla rader och kolumner på platser (tro mig, i provet kan du förväxla en med en tvåa - vad kan vi säga om några rader där), ta bara en titt på bilden:

Bestämning av index för matrisceller

Vad händer? Om vi ​​placerar standardkoordinatsystemet $OXY$ i det övre vänstra hörnet och riktar axlarna så att de täcker hela matrisen, så kan varje cell i denna matris associeras unikt med koordinaterna $\left(x;y \right)$ - detta blir radnumret och kolumnnumret.

Varför är koordinatsystemet placerat exakt i det övre vänstra hörnet? Ja, för det är därifrån vi börjar läsa vilka texter som helst. Det är väldigt lätt att komma ihåg.

Varför pekar $x$-axeln nedåt och inte åt höger? Återigen, det är enkelt: ta standardkoordinatsystemet ($x$-axeln går till höger, $y$-axeln går upp) och rotera den så att den omsluter matrisen. Detta är en 90 graders rotation medurs - vi ser dess resultat på bilden.

I allmänhet kom vi på hur man bestämmer indexen för matriselementen. Låt oss nu ta itu med multiplikation.

Definition. Matriserna $A=\vänster[ m\ gånger n \höger]$ och $B=\vänster[ n\ gånger k \höger]$, när antalet kolumner i den första matchar antalet rader i den andra, kallas konsekventa.

Det är i den ordningen. Man kan vara tvetydig och säga att matriserna $A$ och $B$ bildar ett ordnat par $\left(A;B \right)$: om de är konsekventa i denna ordning, så är det inte alls nödvändigt att $B$ och $A$, d.v.s. paret $\left(B;A \right)$ är också konsekvent.

Endast konsekventa matriser kan multipliceras.

Definition. Produkten av konsekventa matriser $A=\left[ m\times n \right]$ och $B=\left[ n\times k \right]$ är en ny matris $C=\left[ m\times k \right]$ vars element $((c)_(ij))$ beräknas med formeln:

\[((c)_(ij))=\summa\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Med andra ord: för att få ett element $((c)_(ij))$ av matrisen $C=A\cdot B$ måste du ta $i$-raden i den första matrisen, $j$-th kolumnen i den andra matrisen och sedan parvis multiplicera elementen från denna rad och kolumn. Lägg ihop resultaten.

Ja, det är en hård definition. Flera fakta följer omedelbart av det:

1. Matrismultiplikation är generellt sett icke-kommutativ: $A\cdot B\ne B\cdot A$;
2. Multiplikation är dock associativ: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. Och även distributiv: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. Och distributiv igen: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Multiplikationsfördelningen måste beskrivas separat för vänster och höger multiplikatorsumma bara på grund av multiplikationsoperationens icke-kommutativitet.

Om det ändå visar sig att $A\cdot B=B\cdot A$ kallas sådana matriser permuterbara.

Bland alla matriser som multipliceras med något där, finns det speciella - de som, när de multipliceras med valfri matris $A$, återigen ger $A$:

Definition. En matris $E$ kallas identitet om $A\cdot E=A$ eller $E\cdot A=A$. I fallet med en kvadratisk matris $A$ kan vi skriva:

Identitetsmatrisen är en frekvent gäst för att lösa matrisekvationer. Och i allmänhet en frekvent gäst i matrisvärlden. :)

Och på grund av denna $E$ kom någon på allt spel som kommer att skrivas härnäst.

Vad är en invers matris

Eftersom matrismultiplikation är en mycket tidskrävande operation (du måste multiplicera ett gäng rader och kolumner), är konceptet med en invers matris inte heller det mest triviala. Och det behöver lite förklaring.

Nyckeldefinition

Tja, det är dags att veta sanningen.

Definition. Matrisen $B$ kallas inversen av matrisen $A$ if

Den inversa matrisen betecknas med $((A)^(-1))$ (inte att förväxla med graden!), så definitionen kan skrivas om så här:

Det verkar som att allt är extremt enkelt och tydligt. Men när man analyserar en sådan definition uppstår flera frågor omedelbart:

1. Finns det alltid en invers matris? Och om inte alltid, hur ska man då avgöra: när det finns och när det inte finns?
2. Och vem sa att en sådan matris är exakt en? Tänk om det för någon originalmatris $A$ finns en hel skara inverser?
3. Hur ser alla dessa "omvändningar" ut? Och hur räknar man dem egentligen?

När det gäller beräkningsalgoritmerna - vi kommer att prata om detta lite senare. Men vi kommer att svara på resten av frågorna nu. Låt oss ordna dem i form av separata påstående-lemman.

Grundläggande egenskaper

Låt oss börja med hur matrisen $A$ ska se ut för att den ska ha $((A)^(-1))$. Nu ska vi se till att båda dessa matriser måste vara kvadratiska och av samma storlek: $\left[ n\ gånger n \right]$.

Lemma 1. Givet en matris $A$ och dess invers $((A)^(-1))$. Då är båda dessa matriser kvadratiska och har samma ordning $n$.

Bevis. Allt är enkelt. Låt matrisen $A=\vänster[ m\ gånger n \höger]$, $((A)^(-1))=\vänster[ a\ gånger b \höger]$. Eftersom produkten $A\cdot ((A)^(-1))=E$ existerar per definition, är matriserna $A$ och $((A)^(-1))$ konsekventa i den ordningen:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end(align)\]

Detta är en direkt följd av matrismultiplikationsalgoritmen: koefficienterna $n$ och $a$ är "transit" och måste vara lika.

Samtidigt definieras även den inversa multiplikationen: $((A)^(-1))\cdot A=E$, så matriserna $((A)^(-1))$ och $A$ är också konsekventa i denna ordning:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end(align)\]

Utan förlust av allmänhet kan vi alltså anta att $A=\vänster[ m\ gånger n \höger]$, $((A)^(-1))=\vänster[ n\ gånger m \höger]$. Men enligt definitionen av $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, så är dimensionerna på matriserna exakt desamma:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Så det visar sig att alla tre matriserna - $A$, $((A)^(-1))$ och $E$ - är kvadratiska i storlek $\left[ n\ gånger n \right]$. Lemmat är bevisat.

Det är redan bra. Vi ser att endast kvadratiska matriser är inverterbara. Låt oss nu se till att den inversa matrisen alltid är densamma.

Lemma 2. Givet en matris $A$ och dess invers $((A)^(-1))$. Då är denna inversa matris unik.

Bevis. Låt oss börja från motsatsen: låt matrisen $A$ ha minst två instanser av inverser - $B$ och $C$. Då, enligt definitionen, är följande likheter sanna:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(align)\]

Från Lemma 1 drar vi slutsatsen att alla fyra matriserna $A$, $B$, $C$ och $E$ är kvadrater av samma ordning: $\left[ n\ gånger n \right]$. Därför definieras produkten:

Eftersom matrismultiplikation är associativ (men inte kommutativ!), kan vi skriva:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Högerpil B=C. \\ \end(align)\]

Vi har det enda möjliga alternativet: två kopior av den inversa matrisen är lika. Lemmat är bevisat.

Ovanstående resonemang upprepar nästan ordagrant beviset för det inversa elementets unikhet för alla reella tal $b\ne 0$. Det enda betydande tillägget är att ta hänsyn till dimensionen av matriser.

Men vi vet fortfarande ingenting om huruvida någon kvadratisk matris är inverterbar. Här kommer determinanten till vår hjälp - detta är en nyckelegenskap för alla kvadratiska matriser.

Lemma 3 . Givet en matris $A$. Om matrisen $((A)^(-1))$ omvänd till den existerar, är determinanten för den ursprungliga matrisen icke-noll:

\[\vänster| A \right|\ne 0\]

Bevis. Vi vet redan att $A$ och $((A)^(-1))$ är kvadratiska matriser med storleken $\left[ n\ gånger n \right]$. Därför är det möjligt att beräkna determinanten för var och en av dem: $\left| A \right|$ och $\left| ((A)^(-1)) \right|$. Produktens determinant är dock lika med produkten av determinanterna:

\[\vänster| A\cdot B \höger|=\vänster| En \right|\cdot \left| B \höger|\Högerpil \vänster| A\cdot ((A)^(-1)) \right|=\left| En \right|\cdot \left| ((A)^(-1)) \right|\]

Men enligt definitionen av $A\cdot ((A)^(-1))=E$, och determinanten för $E$ är alltid lika med 1, så

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \vänster| A\cdot ((A)^(-1)) \right|=\left| E\right|; \\ & \vänster| En \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \end(align)\]

Produkten av två tal är lika med ett endast om vart och ett av dessa tal skiljer sig från noll:

\[\vänster| En \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Så det visar sig att $\vänster| En \right|\ne 0$. Lemmat är bevisat.

I själva verket är detta krav ganska logiskt. Nu ska vi analysera algoritmen för att hitta den inversa matrisen - och det blir helt klart varför i princip ingen invers matris kan existera med en nolldeterminant.

Men låt oss först formulera en "hjälp" definition:

Definition. En degenererad matris är en kvadratisk matris med storleken $\left[ n\ gånger n \right]$ vars determinant är noll.

Således kan vi hävda att varje inverterbar matris är icke degenererad.

Hur man hittar den inversa matrisen

Nu ska vi överväga en universell algoritm för att hitta inversa matriser. I allmänhet finns det två allmänt accepterade algoritmer, och vi kommer också att överväga den andra idag.

Den som kommer att övervägas nu är mycket effektiv för matriser med storleken $\vänster[ 2\ gånger 2 \höger]$ och - delvis - av storleken $\vänster[ 3\ gånger 3 \höger]$. Men från storleken $\left[ 4\times 4 \right]$ är det bättre att inte använda det. Varför - nu kommer du att förstå allt.

Algebraiska tillägg

Gör dig redo. Nu blir det smärta. Nej, oroa dig inte: en vacker sjuksköterska i kjol, strumpor med spets kommer inte till dig och kommer inte att ge dig en injektion i skinkan. Allt är mycket mer prosaiskt: algebraiska tillägg och Hennes Majestät "Union Matrix" kommer till dig.

Låt oss börja med den viktigaste. Låt det finnas en kvadratisk matris med storleken $A=\vänster[ n\ gånger n \höger]$ vars element heter $((a)_(ij))$. Sedan, för varje sådant element, kan man definiera ett algebraiskt komplement:

Definition. Det algebraiska komplementet $((A)_(ij))$ till elementet $((a)_(ij))$ i $i$th rad och $j$th kolumn i matrisen $A=\left[ n\ gånger n \right]$ är en konstruktion av formen

\[((A)_(ij))=((\vänster(-1 \höger))^(i+j))\cdot M_(ij)^(*)\]

Där $M_(ij)^(*)$ är determinanten för matrisen som erhålls från den ursprungliga $A$ genom att radera samma $i$-th rad och $j$-th kolumn.

Igen. Det algebraiska komplementet till matriselementet med koordinaterna $\left(i;j \right)$ betecknas som $((A)_(ij))$ och beräknas enligt schemat:

1. Först tar vi bort $i$-raden och $j$-th kolumnen från den ursprungliga matrisen. Vi får en ny kvadratisk matris, och vi betecknar dess determinant som $M_(ij)^(*)$.
2. Sedan multiplicerar vi denna determinant med $((\left(-1 \right))^(i+j))$ - till en början kan det här uttrycket verka häpnadsväckande, men i själva verket räknar vi bara ut tecknet framför $M_(ij)^(*)$.
3. Vi räknar – vi får ett specifikt antal. De där. det algebraiska tillägget är bara ett tal, inte någon ny matris, och så vidare.

Själva matrisen $M_(ij)^(*)$ kallas komplementär moll till elementet $((a)_(ij))$. Och i denna mening är ovanstående definition av ett algebraiskt komplement ett specialfall av en mer komplex definition - den som vi övervägde i lektionen om determinanten.

Viktig notering. Faktiskt, i "vuxen" matematik, definieras algebraiska tillägg enligt följande:

1. Vi tar $k$ rader och $k$ kolumner i en kvadratisk matris. Vid deras skärningspunkt får vi en matris med storleken $\left[ k\ gånger k \right]$ — dess determinant kallas en moll av ordningen $k$ och betecknas med $((M)_(k))$.
2. Sedan stryker vi över dessa "utvalda" $k$-rader och $k$-kolumner. Återigen får vi en kvadratisk matris - dess determinant kallas komplementär moll och betecknas med $M_(k)^(*)$.
3. Multiplicera $M_(k)^(*)$ med $((\left(-1 \right))^(t))$, där $t$ är (observera nu!) summan av talen för alla valda rader och kolumner. Detta kommer att vara det algebraiska tillägget.

Ta en titt på det tredje steget: det finns faktiskt en summa på $2k$ termer! En annan sak är att för $k=1$ får vi bara 2 termer - dessa kommer att vara samma $i+j$ - "koordinaterna" för elementet $((a)_(ij))$, för vilket vi letar efter ett algebraiskt komplement.

Så idag använder vi en något förenklad definition. Men som vi får se senare kommer det att räcka mer än väl. Mycket viktigare är följande:

Definition. Unionsmatrisen $S$ till kvadratmatrisen $A=\left[ n\ gånger n \right]$ är en ny matris med storleken $\left[ n\ gånger n \right]$, som erhålls från $A$ genom att ersätta $((a)_(ij))$ med algebraiska tillägg $((A)_(ij))$:

\\Högerpil S=\vänster[ \begin(matris) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ ((A)_(21)) & ((A)_(22)) & ... & ((A)_(2n))) \\ ... & ... (A) & (A) & ...(A) & ...(A) & ((A)_(nn) )) \\\end(matris) \right]\]

Den första tanken som uppstår när man förverkligar denna definition är "det här är hur mycket du måste räkna totalt!" Slappna av: du måste räkna, men inte så mycket. :)

Tja, allt detta är väldigt trevligt, men varför är det nödvändigt? Men varför.

Huvudsats

Låt oss gå tillbaka lite. Kom ihåg att Lemma 3 sa att en inverterbar matris $A$ alltid är icke-singular (det vill säga dess determinant är icke-noll: $\left| A \right|\ne 0$).

Så det omvända är också sant: om matrisen $A$ inte är degenererad, så är den alltid inverterbar. Och det finns till och med ett sökschema $((A)^(-1))$. Kolla in det:

Invers matrissats. Låt en kvadratisk matris $A=\left[ n\ gånger n \right]$ ges, och dess determinant är icke-noll: $\left| En \right|\ne 0$. Då finns den inversa matrisen $((A)^(-1))$ och beräknas med formeln:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

Och nu - ändå, men med läsbar handstil. För att hitta den inversa matrisen behöver du:

1. Beräkna determinanten $\left| A \right|$ och se till att den inte är noll.
2. Kompilera fackföreningsmatrisen $S$, d.v.s. räkna 100500 algebraiska tillägg $((A)_(ij))$ och sätt dem på plats $((a)_(ij))$.
3. Transponera denna matris $S$ och multiplicera den sedan med något tal $q=(1)/(\left| A \right|)\;$.

Och det är allt! Den inversa matrisen $((A)^(-1))$ hittas. Låt oss titta på exempel:

\[\vänster[ \begin(matris) 3 & 1 \\ 5 & 2 \\\end(matris) \höger]\]

Lösning. Låt oss kontrollera reversibiliteten. Låt oss beräkna determinanten:

\[\vänster| En \höger|=\vänster| \begin(matris) 3 & 1 \\ 5 & 2 \\\end(matris) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinanten skiljer sig från noll. Så matrisen är inverterbar. Låt oss skapa en facklig matris:

Låt oss beräkna de algebraiska tilläggen:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\höger|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\höger|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\höger|=3. \\ \end(align)\]

Var uppmärksam: determinanter |2|, |5|, |1| och |3| är bestämningsfaktorerna för matriser med storleken $\vänster[ 1\ gånger 1 \höger]$, inte moduler. De där. om det fanns negativa tal i determinanterna är det inte nödvändigt att ta bort "minus".

Totalt ser vår fackliga matris ut så här:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ((\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \(S)^(T))(array [begin(array)" (35) (r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]\]

OK det är över nu. Problemet löst.

Svar. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Uppgift. Hitta den inversa matrisen:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right]\]

Lösning. Återigen betraktar vi determinanten:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matris) \left(1\cdot 2\cdot 1+\left(-1 \ft)\cdot \cdot \cdot \le 0 \höger)- \\ -\vänster(2\cdot 2\cdot 1+\vänster(-1 \höger)\cdot 0\cdot 1+1\cdot \left(-1 \höger)\cdot 0 \höger) \\\end(matris)= \\ & =\vänster(2+1+0 \(höger) \(4) align )\]

Determinanten skiljer sig från noll - matrisen är inverterbar. Men nu kommer det att bli som mest tinny: du måste räkna så många som 9 (nio, fy fan!) algebraiska tillägg. Och var och en av dem kommer att innehålla $\left[ 2\times 2 \right]$ kvalet. Flög:

\[\begin(matris) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matris) 2 & -1 \\ 0 & 1 \\\end(matris) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matris) 0 & -1 \\ 1 & 1 \\\end(matris) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matris) 0 & 2 \\ 1 & 0 \\\end(matris) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matris) 1 & -1 \\ 0 & 2 \\\end(matris) \right|=2; \\ \end(matris)\]

Kortfattat kommer fackföreningsmatrisen att se ut så här:

Därför blir den omvända matrisen:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matris) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matris) \höger]=\vänster[ \begin(matris)(*)(array)(*)(35) &\ -1 &\ -1 &\ -1 &\ -1 &\ (35) 1 &-2 \\\end(array) \right]\]

Tja, det är allt. Här är svaret.

Svar. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right]$

Som du kan se utförde vi en kontroll i slutet av varje exempel. I detta avseende en viktig anmärkning:

Var inte lat att kolla. Multiplicera den ursprungliga matrisen med den hittade inversen - du bör få $E$.

Det är mycket enklare och snabbare att utföra denna kontroll än att leta efter ett fel i ytterligare beräkningar, när man till exempel löser en matrisekvation.

Alternativt sätt

Som jag sa, den omvända matrissatsen fungerar utmärkt för storlekarna $\left[ 2\times 2 \right]$ och $\left[ 3\times 3 \right]$ (i det senare fallet är det inte så "perfekt" längre), men för större matriser är det rent ut sagt trist.

Men oroa dig inte: det finns en alternativ algoritm som kan användas för att lugnt hitta inversen även för matrisen $\left[ 10\times 10 \right]$. Men, som ofta är fallet, för att överväga denna algoritm, behöver vi lite teoretisk bakgrund.

Elementära transformationer

Bland de olika transformationerna av matrisen finns det flera speciella - de kallas elementära. Det finns exakt tre sådana transformationer:

1. Multiplikation. Du kan ta $i$-th raden (kolumnen) och multiplicera den med valfritt tal $k\ne 0$;
2. Tillägg. Lägg till $i$-th rad (kolumn) vilken annan $j$-th rad (kolumn) som helst multiplicerad med valfritt tal $k\ne 0$ (naturligtvis är $k=0$ också möjligt, men vad är poängen? Ingenting kommer att förändras).
3. Permutation. Ta $i$-th och $j$-th raderna (kolumner) och byt dem.

Varför dessa transformationer kallas elementära (för stora matriser ser de inte så elementära ut) och varför det bara finns tre av dem - dessa frågor ligger utanför ramen för dagens lektion. Därför går vi inte in på detaljer.

En annan sak är viktig: vi måste utföra alla dessa perversioner på den tillhörande matrisen. Ja, ja, du hörde rätt. Nu kommer det en definition till - den sista i dagens lektion.

Bifogad matris

Visst löste man i skolan ekvationssystem med hjälp av additionsmetoden. Tja, där, subtrahera en annan från en rad, multiplicera en rad med ett tal - det är allt.

Så: nu kommer allt att vara sig likt, men redan "på ett vuxet sätt". Redo?

Definition. Låt matrisen $A=\left[ n\ gånger n \right]$ och identitetsmatrisen $E$ av samma storlek $n$ ges. Sedan den associerade matrisen $\left[ A\left| E\rätt. \right]$ är en ny $\left[ n\times 2n \right]$ matris som ser ut så här:

\[\vänster[ A\vänster| E\rätt. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22))) & ... (a)_(22))) & ... ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Kort sagt, vi tar matrisen $A$, till höger tilldelar vi den identitetsmatrisen $E$ av önskad storlek, vi separerar dem med en vertikal stapel för skönhet - här är den bifogade. :)

Vad är haken? Och här är vad:

Sats. Låt matrisen $A$ vara inverterbar. Betrakta den adjoint matrisen $\left[ A\left| E\rätt. \right]$. Om du använder elementära strängtransformationer ta det till formen $\left[ E\left| Ljus. \right]$, dvs. genom att multiplicera, subtrahera och ordna om rader för att erhålla från $A$ matrisen $E$ till höger, då är matrisen $B$ som erhålls till vänster inversen av $A$:

\[\vänster[ A\vänster| E\rätt. \höger]\till \vänster[ E\vänster| Ljus. \höger]\högerpil B=((A)^(-1))\]

Det är så enkelt! Kortfattat ser algoritmen för att hitta den inversa matrisen ut så här:

1. Skriv den associerade matrisen $\left[ A\left| E\rätt. \right]$;
2. Utför elementära strängkonverteringar tills höger istället för $A$ visas $E$;
3. Naturligtvis kommer något också att dyka upp till vänster - en viss matris $B$. Detta blir det omvända;
4. VINST! :)

Naturligtvis mycket lättare sagt än gjort. Så låt oss titta på ett par exempel: för storlekarna $\left[ 3\times 3 \right]$ och $\left[ 4\times 4 \right]$.

Uppgift. Hitta den inversa matrisen:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\]

Lösning. Vi sammanställer den bifogade matrisen:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\]

Eftersom den sista kolumnen i den ursprungliga matrisen är fylld med ettor, subtrahera den första raden från resten:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right])\be \(array) \höger] till \ \ & \to \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\] \end

Det finns inga fler enheter, förutom den första raden. Men vi rör det inte, annars kommer de nyligen borttagna enheterna att börja "multipliceras" i den tredje kolumnen.

Men vi kan subtrahera den andra raden två gånger från den sista - vi får en enhet i det nedre vänstra hörnet:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \\end(array) \\höger]\be \(array) \\höger] \\ & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Nu kan vi subtrahera den sista raden från den första och två gånger från den andra - på detta sätt kommer vi att "nolla ut" den första kolumnen:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \(matris) \(matris) \(matris) \(matris) \(matris) \höger])\be till \ \ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\] \end

Multiplicera den andra raden med −1 och subtrahera den sedan 6 gånger från den första och lägg till 1 gång till den sista:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]| \cdot \left(-1 \right) \right. \\ \ \\\end(matris)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & array \(\\höger) \(\\end) pil \(\\end) 1 \ \\end(matris)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & \\högerände \\end](3 \\)

Det återstår bara att byta rad 1 och 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & -18 & 32 & -13 \\\end(array) \right]\]

Redo! Till höger finns den nödvändiga inversa matrisen.

Svar. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right]$

Uppgift. Hitta den inversa matrisen:

\[\left[ \begin(matris) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matris) \right]\]

Lösning. Återigen komponerar vi den bifogade:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 1 \\\ end(array)\right]\]

Låt oss låna lite, oroa oss för hur mycket vi måste räkna nu ... och börja räkna. Till att börja med "nollställer" vi den första kolumnen genom att subtrahera rad 1 från rad 2 och 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 0 & 1 & 0 & - & 0 & 0 & 0 & - 0 & 0 & 1 \\\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \ \\\end(matris)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & - 0 & 1 & 0 & - 0 & 1 & 0 & - 0 0 \\ 0 & - 5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Vi observerar för många "minus" på rad 2-4. Multiplicera alla tre raderna med -1 och bränn sedan ut den tredje kolumnen genom att subtrahera rad 3 från resten:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & \ -0 & -1 & - & - & 0 & 0 & -1 & - 0 & 0 & 1 \\\end(array) \right]\begin(matris) \ \\ \left| \cdot \left(-1 \right) \right. \\ \vänster| \cdot \left(-1 \right) \right. \\ \vänster| \cdot \left(-1 \right) \right. \\\end(matris)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 2 & 1 & 1 & 0 & 0 & 1 & 1 & 2 5 & 0 & 0 & 0 & -1 \\\end(array) \right]\begin(matris) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matris)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 1 & 0 & 0 & 3 & 0 & 0 & 0 & 1 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Nu är det dags att "steka" den sista kolumnen i den ursprungliga matrisen: subtrahera rad 4 från resten:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 0 & 2 & -1 \\\end(array) \right]\begin(matris) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matris)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -0 & -0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Sista kast: "bränn ut" den andra kolumnen genom att subtrahera rad 2 från rad 1 och 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 2 & 0 & 0 & 5 & 2 & 0 & 2 & -1 \\\end(array) \right]\begin(matris) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matris)\to \\ & \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & - 0 & 0 & 0 & 0 & -6 & - 2 & 0 & 0 & -6 & - 2 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Och igen, identitetsmatrisen till vänster, så inversen till höger. :)

Svar. $\left[ \begin(matris) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & -1 \\\end(matris) \right]$

OK det är över nu. Gör kontrollen själv - jag är skrotad. :)

Liknar inverser i många fastigheter.

Encyklopedisk YouTube

1 / 5

✪ Invers matris (2 sätt att hitta)

✪ Hur man hittar invers matris - bezbotvy

✪ Invers matris #1

✪ Lösa ett ekvationssystem med den inversa matrismetoden - bezbotvy

✪ Omvänd matris

undertexter

Inversa matrisegenskaper

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Var det (\displaystyle \ \det ) betecknar en determinant.
• (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1)) för två kvadratiska inverterbara matriser A (\displaystyle A) Och B (\displaystyle B).
• (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Var (. . .) T (\displaystyle (...)^(T)) betecknar den transponerade matrisen.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1)) för någon koefficient k ≠ 0 (\displaystyle k\not =0).
• E − 1 = E (\displaystyle \ E^(-1)=E).
• Om det är nödvändigt att lösa ett system av linjära ekvationer, (b är en vektor som inte är noll) där x (\displaystyle x)är den önskade vektorn, och om A − 1 (\displaystyle A^(-1)) finns alltså x = A − 1 b (\displaystyle x=A^(-1)b). Annars är antingen dimensionen på lösningsutrymmet större än noll eller så finns det inga alls.

Sätt att hitta den inversa matrisen

Om matrisen är inverterbar kan du använda en av följande metoder för att hitta inversen av matrisen:

Exakta (direkta) metoder

Gauss-Jordan-metoden

Låt oss ta två matriser: sig själv A och singel E. Låt oss ta matrisen A till identitetsmatrisen med Gauss-Jordan-metoden genom att tillämpa transformationer i rader (du kan också tillämpa transformationer i kolumner, men inte i en mix). Efter att ha tillämpat varje operation på den första matrisen, tillämpa samma operation på den andra. När reduktionen av den första matrisen till identitetsformuläret är klar kommer den andra matrisen att vara lika med A -1.

När man använder Gauss-metoden kommer den första matrisen att multipliceras från vänster med en av de elementära matriserna Λ i (\displaystyle \Lambda _(i))(transvektion eller diagonal matris med ettor på huvuddiagonalen, förutom en position):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=\Lambda A =^E-1)ight. Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 − a m − 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 − a m + 1 m / a m m 1 … 0 … 0 … 0 a− m 1 … 0 … 0 … 0 a− m ] (\_ m ) m)=( \begin(bmatrix)1&\prickar &0&-a_(1m)/a_(mm)&0&\prickar &0\\&&&\prickar &&&\\0&\prickar &1&-a_(m-1m)/a_(mm)&0&\prickar &0\_0&mm)&dots &0\_0&mm)&dot ts &0&-a_(m+1 m)/a_(mm)&1&\prickar &0\\&&&\prickar &&&\\0&\prickar &0&-a_(nm)/a_(mm)&0&\prickar &1\end(bmatrix))).

Den andra matrisen efter att ha tillämpat alla operationer kommer att vara lika med Λ (\displaystyle \Lambda ), det vill säga kommer att vara den önskade. Algoritmens komplexitet - O(n 3) (\displaystyle O(n^(3))).

Använda matrisen av algebraiska tillägg

Matris Invers matris A (\displaystyle A), representerar i formen

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Var adj (A) (\displaystyle (\mbox(adj))(A))- bifogad matris;

Algoritmens komplexitet beror på komplexiteten hos algoritmen för beräkning av determinanten O det och är lika med O(n²) O det .

Använder LU/LUP-nedbrytning

Matrisekvation A X = I n (\displaystyle AX=I_(n)) för invers matris X (\displaystyle X) kan ses som en samling n (\displaystyle n) formens system A x = b (\displaystyle Ax=b). Beteckna i (\displaystyle i)-th kolumn i matrisen X (\displaystyle X) genom X i (\displaystyle X_(i)); Sedan A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n),eftersom den i (\displaystyle i)-th kolumn i matrisen I n (\displaystyle I_(n))är enhetsvektorn e i (\displaystyle e_(i)). med andra ord, att hitta den inversa matrisen reduceras till att lösa n ekvationer med samma matris och olika högra sidor. Efter att ha kört LUP-expansionen (tid O(n³)) tar var och en av n ekvationerna O(n²) tid att lösa, så denna del av arbetet tar också O(n³) tid.

Om matrisen A är icke-singular, kan vi beräkna LUP-sönderdelningen för den P A = L U (\displaystyle PA=LU). Låta P A = B (\displaystyle PA=B), B − 1 = D (\displaystyle B^(-1)=D). Sedan, från egenskaperna hos den inversa matrisen, kan vi skriva: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Om vi ​​multiplicerar denna likhet med U och L, kan vi få två likheter i formen U D = L − 1 (\displaystyle UD=L^(-1)) Och D L = U − 1 (\displaystyle DL=U^(-1)). Den första av dessa likheter är ett system av n² linjära ekvationer för n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2))) av vilka de högra sidorna är kända (från egenskaperna hos triangulära matriser). Den andra är också ett system av n² linjära ekvationer för n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2))) av vilka de högra sidorna är kända (även från egenskaperna hos triangulära matriser). Tillsammans bildar de ett system av n² likheter. Med hjälp av dessa likheter kan vi rekursivt bestämma alla n² element i matrisen D. Sedan erhåller vi likheten (PA) −1 = A −1 P −1 = B −1 = D. A − 1 = D P (\displaystyle A^(-1)=DP).

I fallet med användning av LU-sönderdelning krävs ingen permutation av kolumnerna i matrisen D, men lösningen kan divergera även om matrisen A är icke-singular.

Algoritmens komplexitet är O(n³).

Iterativa metoder

Schultz metoder

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_(k+1)=U_(k)\summa _(i=0)^(i=0)^(i=0)^_)(n))\Psi )\Psi _(k)^ses

Uppskattning av fel

Val av initial uppskattning

Problemet med att välja den initiala approximationen i processerna för iterativ matrisinversion som betraktas här tillåter oss inte att behandla dem som oberoende universella metoder som konkurrerar med direktinversionsmetoder baserade till exempel på LU-nedbrytning av matriser. Det finns några rekommendationer för att välja U 0 (\displaystyle U_(0)) för att säkerställa att villkoret uppfylls ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (matrisens spektrala radie är mindre än enhet), vilket är nödvändigt och tillräckligt för processens konvergens. Men i det här fallet måste man först veta uppskattningen för spektrumet för den inverterbara matrisen A eller matrisen A A T (\displaystyle AA^(T))(Nämligen, om A är en symmetrisk positiv definitiv matris och ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), då kan du ta U 0 = α E (\displaystyle U_(0)=(\alpha )E), Var ; om A är en godtycklig icke-singular matris och ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), anta då U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), var också α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); Naturligtvis kan situationen förenklas och med hjälp av det faktum att ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), sätta U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|))))). För det andra, med en sådan specifikation av den initiala matrisen, finns det ingen garanti för det ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|) kommer att vara liten (kanske till och med ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), och en hög konvergenshastighet kommer inte att vara omedelbart uppenbar.

Exempel

Matris 2x2

Det går inte att tolka uttryck (syntaxfel): (\displaystyle \mathbf(A)^(-1) = \begin(bmatrix) a & b \\ c & d \\ \end(bmatrix)^(-1) = \frac(1)(\det(\mathbf(A))) \begin& \!\!-b \\ -c & \end =(b \\ -c)\end =(b \\ -c) begin(bmatrix) \,\,\,d & \!\!-b\\ -c & \,a \\ \end(bmatrix).)

Inversionen av en 2x2-matris är endast möjlig under förutsättning att a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

För invers matris det finns en passande analogi med ett tals ömsesidiga. För varje nummer a, som inte är lika med noll, finns det ett tal b att arbetet a Och b lika med ett: ab= 1 . siffra b kallas den reciproka av ett tal b. Till exempel, för talet 7, är inversen talet 1/7, eftersom 7*1/7=1.

invers matris , som krävs för att hittas för en given kvadratisk matris A, en sådan matris kallas

produkten genom vilken matriserna A till höger finns identitetsmatrisen, dvs.
. (1)

En identitetsmatris är en diagonal matris där alla diagonala poster är lika med en.

Hitta den inversa matrisen- ett problem som oftast löses med två metoder:

• metoden för algebraiska tillägg, där det krävs att hitta determinanter och transponera matriser;
• den Gaussiska elimineringsmetoden, som kräver elementära transformationer av matriser (lägg till rader, multiplicera rader med samma antal, etc.).

För den som är särskilt nyfiken finns det andra metoder, till exempel metoden linjära transformationer. I den här lektionen kommer vi att analysera de tre nämnda metoderna och algoritmer för att hitta den inversa matrisen med dessa metoder.

Sats.För varje icke-singular (icke-singular, icke-singular) kvadratisk matris kan man hitta en invers matris, och dessutom bara en. För en speciell (degenererad, singular) kvadratisk matris existerar inte den inversa matrisen.

Den kvadratiska matrisen kallas icke-speciell(eller icke degenererad, icke-singular) om dess determinant inte är lika med noll, och särskild(eller degenererad, singularis) om dess determinant är noll.

Den inversa matrisen kan bara hittas för en kvadratisk matris. Naturligtvis kommer den inversa matrisen också att vara kvadratisk och av samma ordning som den givna matrisen. En matris för vilken en invers matris kan hittas kallas en inverterbar matris.

Hitta den omvända matrisen genom Gaussisk eliminering av okända

Det första steget för att hitta den inversa matrisen genom gaussisk eliminering är att tilldela matrisen A identitetsmatris av samma ordning, som skiljer dem åt med en vertikal stapel. Vi får en dubbel matris. Multiplicera båda delarna av denna matris med , då får vi

,

Algoritm för att hitta den inversa matrisen genom Gauss eliminering av okända

1. Till matrisen A tilldela en identitetsmatris av samma ordning.

2. Transformera den resulterande dubbla matrisen så att identitetsmatrisen erhålls i dess vänstra del, då kommer den inversa matrisen automatiskt att erhållas i den högra delen i stället för identitetsmatrisen. Matris A på vänster sida omvandlas till identitetsmatrisen genom elementära transformationer av matrisen.

2. Om i färd med matristransformation A i identitetsmatrisen i valfri rad eller kolumn kommer det bara att finnas nollor, då är matrisens determinant lika med noll, och därför matrisen A kommer att vara degenererad och den har ingen invers matris. I detta fall upphör ytterligare sökning av den inversa matrisen.

Exempel 2 För matris

hitta den inversa matrisen.

och vi kommer att omvandla det så att identitetsmatrisen erhålls på vänster sida. Låt oss börja omvandlingen.

Multiplicera den första raden i vänster och höger matris med (-3) och lägg till den till den andra raden, och multiplicera sedan den första raden med (-4) och lägg till den till den tredje raden, då får vi

.

För att, om möjligt, det inte finns några bråktal under efterföljande transformationer, kommer vi först att skapa en enhet i den andra raden på vänster sida av den dubbla matrisen. För att göra detta, multiplicera den andra raden med 2 och subtrahera den tredje raden från den, då får vi

.

Låt oss lägga till den första raden till den andra och sedan multiplicera den andra raden med (-9) och lägga till den till den tredje raden. Då får vi

.

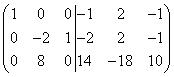Dela sedan den tredje raden med 8

.

Multiplicera den tredje raden med 2 och lägg till den i den andra raden. Det visar sig:

.

Om vi ​​byter plats på andra och tredje raden får vi äntligen:

.

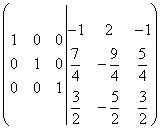Vi ser att identitetsmatrisen erhålls på vänster sida, därför erhålls den omvända matrisen på höger sida. Således:

.

Du kan kontrollera korrektheten av beräkningarna genom att multiplicera den ursprungliga matrisen med den hittade inversa matrisen:

Resultatet bör vara en omvänd matris.

online-kalkylator för att hitta den inversa matrisen .

Exempel 3 För matris

hitta den inversa matrisen.

Lösning. Kompilera en dubbel matris

och vi kommer att förvandla det.

Vi multiplicerar den första raden med 3 och den andra med 2 och subtraherar från den andra, och sedan multiplicerar vi den första raden med 5, och den tredje med 2 och subtraherar från den tredje raden, då får vi

.

Vi multiplicerar den första raden med 2 och adderar den till den andra, och subtraherar sedan den andra från den tredje raden, då får vi

.

Vi ser att på den tredje raden på vänster sida visade sig alla element vara lika med noll. Därför är matrisen degenererad och har ingen invers matris. Vi stoppar ytterligare fynd av omvänd maria.

Du kan kolla lösningen med

Matris A -1 kallas den inversa matrisen med avseende på matris A, om A * A -1 \u003d E, där E är identitetsmatrisen av n:te ordningen. Den inversa matrisen kan bara existera för kvadratiska matriser.

Serviceuppdrag. Genom att använda den här tjänsten online kan du hitta algebraiska tillägg, transponerad matris A T , unionsmatris och invers matris. Lösningen utförs direkt på sajten (online) och är gratis. Beräkningsresultaten presenteras i en rapport i Word-format och i Excel-format (det vill säga det går att kontrollera lösningen). se designexempel.

Instruktion. För att få en lösning måste du ange dimensionen på matrisen. Därefter, i den nya dialogrutan, fyll i matrisen A .

Se även Invers matris med Jordan-Gauss-metoden

Algoritm för att hitta den inversa matrisen

1. Hitta den transponerade matrisen A T .
2. Definition av algebraiska tillägg. Ersätt varje element i matrisen med dess algebraiska komplement.
3. Sammanställning av en invers matris från algebraiska tillägg: varje element i den resulterande matrisen delas med determinanten för den ursprungliga matrisen. Den resulterande matrisen är inversen av den ursprungliga matrisen.

Nästa invers matrisalgoritm liknande den föregående, förutom några steg: först beräknas de algebraiska komplementen och sedan bestäms unionsmatrisen C.

1. Bestäm om matrisen är kvadratisk. Om inte, så finns det ingen invers matris för det.
2. Beräkning av determinanten för matrisen A . Om det inte är lika med noll fortsätter vi lösningen, annars existerar inte den inversa matrisen.
3. Definition av algebraiska tillägg.
4. Fylla i den fackliga (ömsesidiga, angränsande) matrisen C .
5. Sammanställning av den inversa matrisen från algebraiska tillägg: varje element i den adjoint matrisen C delas med determinanten för den ursprungliga matrisen. Den resulterande matrisen är inversen av den ursprungliga matrisen.
6. Gör en kontroll: multiplicera originalet och de resulterande matriserna. Resultatet bör vara en identitetsmatris.

Exempel #1. Vi skriver matrisen i formen:

Algebraiska tillägg. ∆ 1,2 = -(2 4-(-2 (-2))) = -4 ∆ 2,1 = -(2 4-5 3) = 7 ∆ 2,3 = -(-1 5-(-2 2)) = 1 ∆ 3,2 = -(-1 (-2)-2 3) = 4

A -1 =

0,6 -0,4 0,8 0,7 0,2 0,1 -0,1 0,4 -0,3

En annan algoritm för att hitta den inversa matrisen

Vi presenterar ett annat schema för att hitta den inversa matrisen.

1. Hitta determinanten för den givna kvadratmatrisen A .
2. Vi hittar algebraiska tillägg till alla element i matrisen A .
3. Vi skriver in de algebraiska komplementen av elementen i raderna i kolumnerna (transposition).
4. Vi delar varje element i den resulterande matrisen med determinanten för matrisen A .

Som du kan se kan transponeringsoperationen tillämpas både i början, över den ursprungliga matrisen och i slutet, över de resulterande algebraiska tilläggen.

Ett speciellt fall: Det omvända, med avseende på identitetsmatrisen E, är identitetsmatrisen E.