نظرية المعاملة بالمثل للوظائف الممكنة. نظرية ماكسويل (نظرية حول المعاملة بالمثل لإزاحة الوحدات). ترتيب التنفيذ ومعالجة النتائج
دع الشعاع له حالتان:

حيث ∆ 12 هي الإزاحة عند النقطة 1 من القوة المؤثرة عند النقطة 2.
∆ 21 - الإزاحة عند النقطة 2 من القوة المطبقة عند النقطة 1.
لاشتقاق النظرية ، نقوم أولاً بتحميل الحزمة بالقوة F 1 ، ثم بالقوة F 2

الشغل المنجز هو: W = W 11 + W 22 + W 12 = + + F 1 ∙ ∆ 12

ث \ u003d W 22 + W 11 + W 21 \ u003d + + F 2 ∙ ∆ 21
لأن القوى هي نفسها ، فالعمل هو نفسه ، يلي: F 1 ∙ ∆ 12 = F 2 ∙ ∆ 21 - نظرية العمل بالمثل (نظرية بيتي): عمل قوى الحالة الأولى لتحريك الحالة الثانية يساوي عمل قوى الدولة الثانية لتحريك الحالة الأولى.
إذا قبلنا F 1 \ u003d F 2 \ u003d 1 (قيمة بدون أبعاد) ، فإننا نحصل على نظرية حول المعاملة بالمثل للإزاحة (نظرية ماكسويل): δ 12 \ u003d δ 21 - الإزاحة من قوة الوحدة. ث: الحركة عند نقطة تطبيق قوة الوحدة الأولى في اتجاهها الناتجة عن قوة الوحدة الثانية تساوي الحركة عند نقطة تطبيق قوة الوحدة الثانية في اتجاهها الناتجة عن قوة الوحدة الأولى.
10. طريقة تحليل الرسم البياني لحل تكامل Mohr (طريقة Vereshchagin)
إذا تم تحميلها. sys-لدينا عدد من الأقسام ذات الانحناءات المختلفة. لحظات ، فإن حساب التكامل صعب إلى حد ما. لذلك ، يتم استخدام طريقة Vereshchagin.
دع البضائع. يحتوي مخطط اللحظات على مخطط منحني ووحدة. مؤامرة بيند. اللحظات لها شكل خطي ، وفي هذه الحالة ، تكامل موهر ![]() .(خاتمة)
.(خاتمة)
![]() ;
dw = S y - لحظة ثابتة لمنطقة الشحن. قطع اللحظات حول المحور ص.
;
dw = S y - لحظة ثابتة لمنطقة الشحن. قطع اللحظات حول المحور ص.
العزم الثابت لأي شكل يساوي ناتج المنطقة والمسافة من المحور إلى مركز ثقل الشكل حيث w هي مساحة مخطط الشحن MF ؛ Z ج - المسافة إلى مركز الجاذبية.
;
ومع ذلك ، وجود قيمة اللحظة من حمل واحد تحت مركز ثقل الحمل. الرسوم البيانية: نظرًا لأنه يمكن تطبيق عدة أحمال على الحزمة ، يتم تحديد الإزاحة لكل قسم من الشعاع ![]() - صيغة Vereshchagin ، أي أن الإزاحة تساوي مساحة الرسم البياني المنحني لكل تنسيق من الرسم التخطيطي المنحني المستقيم الموجود أسفل مركز الثقل. في الحسابات العملية ، مساحة البضائع. تنقسم المخططات إلى رسوم بيانية بسيطة (رسومات).
- صيغة Vereshchagin ، أي أن الإزاحة تساوي مساحة الرسم البياني المنحني لكل تنسيق من الرسم التخطيطي المنحني المستقيم الموجود أسفل مركز الثقل. في الحسابات العملية ، مساحة البضائع. تنقسم المخططات إلى رسوم بيانية بسيطة (رسومات).
نظم غير محددة إحصائيا طريقة الحساب. النظام الأساسي وما يعادله.
الحزم غير المحددة بشكل ثابت (الإطارات) تسمى. الحزم (الإطارات) التي لا يمكن فيها تحديد جميع ردود الفعل غير المعروفة للدعامات باستخدام معادلات الاستاتيكات فقط ، نظرًا لأن لديها خطوط اتصال (تفاعلات). يتم تحديد درجة عدم اليقين الثابت بالفرق بين عدد التفاعلات غير المعروفة والمعادلات الساكنة.

تحتوي الحزم على 4 وصلات دعم ، أي 4 مناطق دعم. احصائيات أور-ث لنظام مسطح. يمكنك عمل 3 ، وبالتالي فإن الشعاع هو yavl. 1 وقت ثابت لا يمكن تحديده. من أجل الكشف عن ثابت إلى أجل غير مسمى ، فمن الضروري. إلى احصائيات ur-th لتقديم المزيد. Ur-e يعتمد على حركة النظام. يتم تحديد عددهم. درجة اللاحتمية الثابتة. إذا كان هناك العديد من المجاهيل الخطية ، فقم بإضافة. ur-I state-Xia استنادًا إلى ظروف التشوه (الانحرافات) على دعامة الحزمة باستخدام طريقة المعلمات الأولية.
شركات احصائيات Ur-I وإضافة. Ur-I لشعاع معين: Z = 0 ؛ ص = 0 ؛ م (ب) = 0.
يضيف. Ur-e نكتب من الشرط أن الانحراف على الدعم B = 0. EIY (B) = 0. بعض الأنظمة. درجة ثابتة غير محدد عالية (عوارض صلبة). يضيف. يتم تجميع ur-e بناءً على ظروف التشوه (زوايا دوران القسم) على الدعامات الوسيطة للحزمة باستخدام طريقة القوة. من المحلول المشترك لإحصاءات ur-th و ur-th الإضافي ، نجد جميع ردود الفعل غير المعروفة
بعد تحديد درجة عدم التحديد الثابت ، يتم تجميع النظام الأساسي. يُفهم النظام الرئيسي على أنه نظام محدد ثابتًا ، يتم الحصول عليه من نظام غير محدد بشكل ثابت عن طريق تجاهل الوصلات الخطية.




اتصالات 6 ، معادلات احصائيات 3. 6-3 = 3 - 3 مرات نظام نيوبريد ثابت
هناك العديد من الأنظمة الأساسية للاختيار من بينها. عند اختيار النظام الرئيسي ، من الضروري أن يكون ثابتًا هندسيًا وفوريًا.
"معدل هندسيًا" ، "تم تعديله على الفور"
تشمل الأنظمة التي تم تغييرها على الفور الأنظمة التي تتقاطع فيها تفاعلات الدعم عند نقطة واحدة. إذا كان النظام الرئيسي قم بتطبيق التوصيلات الساقطة والحمل ، ثم نحصل على نظام مكافئ.
دعونا ننظر في النظام الرئيسي الأول. رسم
دعونا ننظر في النظام الرئيسي الثاني. رسم
أساسيات طريقة القوة.
يتم حساب طريقة القوة في ما يلي. طلب:
1) تحديد درجة اللاحتمية الثابتة
2) نختار الأنظمة الرئيسية والمكافئة. التخلص من خطوط الاتصال واستبدالها بقوى مجهولة X1 و X2 و X3.
3) اكتب شروط تكافؤ الأنظمة المعطاة والمكافئة من حيث الإزاحة
نظام معين  معادل
معادل
إذا لم يكن لنظام معين حركة في اتجاه قوى غير معروفة X1 ، x2 ، X3 ، فإن شروط التكافؤ ستبدو كما يلي: = 0 ، = 0.
نعبر عن عمليات النزوح هذه من كل قوة غير معروفة ومن الحمل الخارجي
الحركات:
أما بالنسبة للمجهولين X1 و X2 و X3 ، فيمكن تمثيل تأثيرهم على الحركة على النحو التالي:
X1 ؛ = X2 ؛ = X3 أي تعريف عمليات النزوح من الوحدات. القوى المطبقة في الاتجاه تقوم الوصلات بضربها بالقوى المجهولة المقابلة X. بعد ذلك ، ستأخذ عمليات النزوح في اتجاه 3 اتصالات غير معروفة الشكل.
نظرية العمل بالمثل. نظرية المعاملة بالمثل للتهجير
لنأخذ في الاعتبار نظامًا مشوهًا خطيًا في حالتين مختلفتين تقابلان حمولتين مختلفتين (الشكل 5.15) ، ولتبسيط الحسابات ، دعونا نفكر في حزمة بسيطة ثنائية الدعم محملة بالتتابع بواسطة قوتين مركزة.
الشكل 15. ترتيب مباشر وعكسي لتطبيق الحمل
نحصل على معادلة إجمالي العمل للترتيب المباشر والعكسي لتطبيق الأحمال
يُطلق على العمل الذي تقوم به قوة ما على عمليات النزوح التي تسببها قوة أو قوى أخرى العمل الإضافي.
وفقًا لنظرية المعاملة بالمثل ، فإن عمل قوى الدولة الأولى لتحريك الحالة الثانية يساوي عمل قوى الحالة الثانية لتحريك الحالة الأولى.
وبالمثل ، يمكن أيضًا إثبات المعاملة بالمثل للعمل الإضافي للقوى الداخلية.
الشكل 16. المعاملة بالمثل للعمل الإضافي للقوى الداخلية.
باستخدام قانون حفظ الطاقة ، يمكن إثبات أن العمل الإضافي للقوى الخارجية يساوي في القيمة المطلقة العمل الإضافي للقوى الداخلية:
مع الأخذ
نحصل على نظرية حول المعاملة بالمثل لعمليات الإزاحة.
إن إزاحة نقطة تطبيق قوة الوحدة في اتجاهها ، والناجمة عن قوة الوحدة الثانية ، تساوي إزاحة نقطة تطبيق قوة الوحدة الثانية في اتجاه الأخير ، الناتج عن فعل قوة الوحدة الأولى.
تحديد النزوح بطريقة موهر
بدلاً من نظام القوى F 1 و F 2 ، نقدم حالات الشحن والحالات المساعدة:
الشكل 17. إدخال البضائع والحالات المساعدة
دعونا نكتب نظرية العمل بالمثل لهاتين الحالتين:
بعد جمع المقاطع الفردية من الحزمة ، نحصل على تكامل Mohr
مثال 5.2.ضع في اعتبارك مثالاً لاستخدام تكامل Mohr لتحديد حالات الإزاحة لشعاع ناتئ محمل بقوة مركزة
الشكل 18. بناء الحمل ومخطط مساعد لحزمة ناتئ
نستخدم تكامل موهر.
في الممارسة العملية ، من الصعب استخدام هذا النهج. يتم التغلب على هذه الصعوبة من خلال تنظيم التكامل ، يتم تنفيذ التكامل بسهولة على الكمبيوتر.
طريقة الرسم البياني التحليلي لتحديد الإزاحة أثناء الانحناء. طريقة Vereshchagin
نقدم حالتين مبسّطتين:
دالة خطية داخل القسم المدروس.
الشكل 19 الحساب التحليلي للرسم البياني لتكامل موهر
التكامل الأخير هو اللحظة الثابتة للشكل ABCD حول المحور y. عمل
يمثل الإحداثي المأخوذ على الرسم البياني الإضافي تحت مركز ثقل الحمولة.
حيث n هو رقم القسم.
مثال 5.3.ضع في اعتبارك شعاع الكابول مرة أخرى
الشكل 20. استخدام طريقة Vereshchagin لشعاع ناتئ
حالات أكثر صعوبة:
1. ضرب شبه منحرف بواسطة شبه منحرف
أرز. 21. اضرب شبه منحرف في شبه منحرف
لمضاعفة شبه منحرف في شبه منحرف ، يمكنك متابعة ضرب مستطيل في شبه منحرف ومثلث في شبه منحرف.
تعريف ضرب مستطيل في شبه منحرف يعني أننا نأخذ A f على طول المستطيل ، و M k c على طول شبه منحرف.
تعمل قاعدة التقليب فقط على المخططات الخطية.
2. قطعة مكافئ
الشكل 22. مساحة وموقع مركز الثقل لقطعة مكافئ
3. مثلث مكافئ مقعر
الشكل 23. مساحة وموقع مركز الثقل لمثلث مكافئ مقعر
4. مثلث محدب
الشكل 24. مساحة وموقع مركز الثقل لمثلث مكافئ محدب
5. شبه منحرف محدب مكافئ.
الشكل 25. تقسيم المناطق وموقع مراكز الثقل لشبه منحرف محدب مكافئ
مثال: 5.4.دعونا نفكر في حالة أكثر تعقيدًا لتحميل حزمة ناتئ ، عندما تعمل جميع أنواع الأحمال الخارجية الثلاثة. من الضروري تحديد أقصى زاوية دوران للحزمة
أرز. شعاع ناتئ مع عمل متزامن لثلاثة أحمال
ط الطريق. لنستبدل الشكل M f بمجموعة من الأشكال الأبسط.
أي رأس القطع المكافئ خارج الحزمة.
لإنشاء مخطط إضافي ، يجب عليك:
1. النظر في شعاع بدون أحمال خارجية.
2. عند نقطة معينة ، قم بتطبيق F = 1 أو M = 1 ، على التوالي ، لتحديد الانحراف أو زاوية الدوران. اتجاه عمل الأحمال الخارجية تعسفي.
3. بالنظر إلى حمل الوحدة على أنه خارجي ، فإننا نحدد التفاعلات ونبني الرسوم البيانية.
ستتخذ صيغة تحديد زاوية الدوران بطريقة Vereshchagin الشكل التالي
حيث - الإحداثي المأخوذ على الرسم التخطيطي الإضافي M إلى تحت مركز ثقل مخطط الشحن - مع مراعاة تقسيم مخطط الشحن إلى أرقام أولية
عند إنشاء محور شعاع منحني ، نستخدم:
1. علامة النزوح المعمم. بالنسبة للحالة المدروسة ، يتم تدوير النقطة في اتجاه عقارب الساعة.
2. استخدم علامة لحظة الانحناء على مخطط الحمل.
يظهر عرض تقريبي للمحور المنحني للحزمة في الشكل. 5.24.
الطريقة الثانية. باستخدام مبدأ التراكب.
أرز باستخدام مبدأ التراكب





بيان نظرية المعاملة بالمثل في العمل (نظرية بيتي)، تم إثباته في عام 1872 بواسطة E.Betti: العمل المحتمل لقوى الدولة الأولى على عمليات النزوح المقابلة التي تسببها قوى الحالة الثانية يساوي العمل المحتمل لقوى الحالة الثانية على عمليات النزوح المقابلة التي تسببها قوات الدولة الأولى.
24- نظرية المعاملة بالمثل لعمليات التشرد (ماكسويل)
|
|
|
اسمحوا و. نظرية المعاملة بالمثل لعمليات الإزاحةمع الأخذ في الاعتبار التعيين المقبول للإزاحة من وحدة القوة ، فإن لها الشكل: تم إثبات نظرية المعاملة بالمثل للإزاحة بواسطة ماكسويل. بيان نظرية المعاملة بالمثل: إزاحة نقطة تطبيق وحدة القوة الأولى ، الناتجة عن عمل القوة الثانية ، تساوي إزاحة نقطة تطبيق قوة الوحدة الثانية ، الناتجة عن عمل الوحدة الأولى من القوة
25. نظرية رايلي في المعاملة بالمثل من ردود الفعل. 

26. نظرية Gvozdev في المعاملة بالمثل من النزوح وردود الفعل.


27. تحديد حالات النزوح من الحمل. صيغة موهر.

صيغة مورا


28- تحديد حالات النزوح من تأثيرات درجة الحرارة ومن التشريد.
تأثير درجة الحرارة.


مسودة


29. حكم Vereshchagin. صيغة الضرب شبه المنحرف ، صيغة سيمبسون.


صيغة شبه منحرف.
![]()
صيغة الضرب لشبه المنحنيات المنحنية
31. خصائص الأنظمة غير المحددة إستاتيكياً.
لتحديد القوى وردود الفعل ، فإن معادلات الإحصائيات ليست كافية ، فمن الضروري إشراك معادلات استمرارية التشوه والتشريد.
تعتمد الجهود وردود الفعل على نسبة صلابة العناصر الفردية.
تؤدي التغيرات في درجة الحرارة واستقرار الدعم إلى ظهور قوى داخلية.
في حالة عدم وجود حمل ، من الممكن حدوث حالة من الإجهاد الذاتي.
32. تحديد درجة ثابتة اللاحتمية ، مبادئ اختيار النظام الرئيسي لأسلوب القوات.
للأنظمة غير المحددة بشكل ثابت W<0
يتم تحديد عدد الاتصالات الإضافية بواسطة الصيغة:
L = -دبليو+ 3 ك,
حيث W هو عدد المعلمات الهندسية المستقلة التي تحدد موضع الهيكل على المستوى دون مراعاة تشوه الهيكل (عدد درجات الحرية) ، K هو عدد الخطوط المغلقة (الخطوط العريضة التي يوجد فيها لا مفصلة).
دبليو\ u003d 3D - 2Sh - Co
صيغة Chebyshev لتحديد درجة الحرية ، حيث D هو عدد الأقراص ، W هو عدد المفصلات ، Co هو عدد قضبان الدعم.
يجب أن يكون OSMS ثابتًا هندسيًا.
يجب أن يكون قابلاً للتحديد بشكل ثابت (إزالة التوصيلات الإضافية L).
يجب أن يكون هذا النظام سهل الحساب.
إذا كان النظام الأصلي متماثلًا ، فسيتم اختيار OSMS باعتباره متماثلًا إن أمكن.
33. المعادلات المتعارف عليها لطريقة القوة ومعناها المادي.
المعادلات المتعارف عليها:

المعنى المادي:
يجب أن تكون الحركة الإجمالية في اتجاه كل وصلة بعيدة = 0
34. حساب معاملات المعادلات المتعارف عليها ومعناها المادي والتحقق من صحة المعاملات الموجودة.

التحرك في اتجاه هذا الاتصال البعيد الناجم عن قوة وحدة جيتا.

الحركة في اتجاه هذا الاتصال البعيد ناتجة عن حمل خارجي.


للتحقق من صحة المعاملات التي تم العثور عليها ، تحتاج إلى استبدالها في نظام المعادلات المتعارف عليها وإيجاد X1 و X2.

عمل القوة الأولى على إزاحة نقطة تطبيقها الناتجة عن القوة الثانية يساوي عمل القوة الثانية على إزاحة نقطة تطبيقها الناتجة عن القوة الأولى.
(دائمًا ما تكون الأنظمة المرنة الخطية متحفظة إذا كانت محملة بقوى محافظة ، أي قوى لها إمكانات).
كنموذج نظام ، نختار شعاع ناتئ. سيتم الإشارة إلى النزوح على أنه إزاحة في اتجاه القوة التي تسببها القوة.
نحمل النظام أولاً بقوة ثم نطبق القوة. سيتم كتابة عمل القوى المطبقة على النظام:
![]()
(لماذا المصطلحين الأولين لهما عامل وآخر لا؟)
ثم نطبق القوة الأولى والثانية -.
لأن النظام محافظ ، وأيضًا لأن الحالتين الأولي والنهائي في كلتا الحالتين تتطابقان ، فيجب أن يكون العمل متساويًا ، مما يعني
إذا وضعنا ذلك ، فسنحصل على حالة خاصة من نظرية بيتي - نظرية المعاملة بالمثل للإزاحة.
سنقوم بتعيين عمليات النزوح التي تسببها قوى الوحدة (معنى المؤشرات هو نفسه). ثم
سلالة الطاقة المحتملة للطائرة
نظام القضيب.
سننظر في نظام مسطح ، أي نظام تكمن قضبانه وجميع القوى في نفس المستوى. في قضبان مثل هذا النظام ، في الحالة العامة ، يمكن أن تحدث مع عوامل القوة الداخلية:
النظام المرن ، كونه مشوهًا ، يراكم الطاقة (الطاقة المرنة) التي تسمى سلالة الطاقة المحتملة.
 أ) إجهاد الطاقة المحتملة في التوتر والضغط.
أ) إجهاد الطاقة المحتملة في التوتر والضغط.
ستكون الطاقة الكامنة المتراكمة في عنصر صغير بطول dz مساوية لشغل القوى المطبقة على هذا العنصر
![]()
الطاقة الكامنة للقضيب: 
تعليق.وهي قيم ثابتة اختياريًا.
ب) الطاقة الكامنة في الانحناء.

للقضيب: 
ج) تسبب قوى القص نوبات ، وهي تتوافق مع
القص الطاقة الكامنة. ومع ذلك ، تكون هذه الطاقة صغيرة في معظم الحالات ولن نأخذها في الاعتبار.
تعليق.استخدمنا قضبان مستقيمة كأشياء قيد الدراسة ، ولكن النتائج التي تم الحصول عليها تنطبق أيضًا على قضبان منحنية ذات انحناء صغير ، حيث يكون نصف قطر الانحناء أكبر من ارتفاع القسم بحوالي 5 مرات أو أكثر.
يمكن كتابة الطاقة الكامنة لنظام القضيب: ![]()
هنا ، يتم أخذ الظرف في الاعتبار أنه أثناء التوتر والضغط ، لا تدور الأقسام ، وبالتالي ، فإن لحظات الانحناء لا تؤدي عملاً ، وعند الانحناء ، لا تتغير المسافة على طول المحور بين الأقسام المجاورة وعمل القوى العادية هو صفر. أولئك. يمكن حساب الطاقة الكامنة للانحناء وضغط التوتر بشكل مستقل.
تعني علامات التحفيز أن الطاقة الكامنة محسوبة للنظام بأكمله.
نظرية كاستيلانو.
يوضح التعبير (3) أن الطاقة الكامنة للتشوه هي دالة تربيعية متجانسة ، وهذه بدورها تعتمد خطيًا على القوى المؤثرة على النظام ، وبالتالي فهي دالة تربيعية للقوى.
![]()
نظرية.المشتق الجزئي للطاقة الكامنة فيما يتعلق بالقوة يساوي إزاحة نقطة تطبيق هذه القوة في اتجاه الأخير.
دليل:
دعونا تكون الطاقة الكامنة المقابلة لقوى النظام دعونا ننظر في حالتين.
1) أولاً ، يتم تطبيق جميع القوى ثم يتلقى أحدهم زيادة صغيرة ، ثم إجمالي الطاقة الكامنة يساوي:
2) أولاً يتم تطبيق القوة ثم يتم تطبيق القوى.في هذه الحالة ، الطاقة الكامنة هي:
![]()
لأن الحالة الأولية والنهائية هي نفسها في كلتا الحالتين ، والنظام محافظ ، ثم الطاقات المحتملة يجب أن تكون متساوية ![]()
نحصل على تجاهل الطلب الثاني الصغير
موهر لا يتجزأ.
أعطتنا نظرية كاستيلانو القدرة على تحديد الإزاحة. تستخدم هذه النظرية لإيجاد الإزاحة في الصفائح والأصداف. ومع ذلك ، فإن حساب الطاقة الكامنة هو إجراء مرهق ، وسنقوم الآن بتحديد طريقة أبسط وأكثر عمومية لتحديد عمليات الإزاحة في أنظمة القضيب.
 دعنا نعطي نظام قضيب تعسفي ونحتاج إلى تحديد حركة نقطة في الاتجاه الذي تسببه جميع قوى النظام -
دعنا نعطي نظام قضيب تعسفي ونحتاج إلى تحديد حركة نقطة في الاتجاه الذي تسببه جميع قوى النظام -
8 صفحات (ملف Word)
عرض كل الصفحات


15. الطاقة الكامنة للتشوه في الانحناء.
في الانحناء ، وكذلك في أنواع التشوه الأخرى ، يتم إنفاق العمل الناتج عن القوى الخارجية على تغيير الطاقة الكامنة للقضيب المشوه.
عمل اللحظة الخارجية أثناء التشوه المرن للقضيب:
أين زاوية دوران المقطع عند نقطة التطبيق في الوقت الحالي.

يتم تحديد العمل الأولي لعزم الانحناء (الداخلي) من التعبير (عن طريق القياس مع حالة ضغط التوتر):
![]() ، ولكن عند الانحناء لدينا:.
، ولكن عند الانحناء لدينا:.
يتم تحديد الانحناء ، باعتباره مقلوب نصف قطر الانحناء ، من التعبير:
![]() حيث: - معامل المرونة من النوع الأول.
حيث: - معامل المرونة من النوع الأول.
لحظة القصور الذاتي للقسم حول المحور المحايد للقسم.
لذلك يمكننا أن نكتب:
![]() .
.
إجمالي عمل لحظات الانحناء لشعاع طويل ل:
 .
.
يتم تحديد الطاقة الكامنة للثني ، التي تساوي عمل القوى الداخلية ، المأخوذة بعلامة معاكسة ، من التعبير:
 .
.
إن إضافة الطاقة الكامنة بسبب القص (للحالة العامة ، ليس الانحناء المباشر ، ولكن الانحناء المستعرض) ، يتوافق مع عمل القوة المستعرضة. ومع ذلك ، فإن هذه الإضافة صغيرة من حيث القيمة المطلقة وعادة ما يتم إهمالها في الحسابات العملية.
16. نظرية المعاملة بالمثل في العمل والمعاملة بالمثل من التشرد.
ضع في اعتبارك نظامًا مرنًا مشوهًا خطيًا في حالتين مختلفتين تقابلان حملين مختلفين P1و P2(الشكل 47). في هذه الحالة ، يتم تحميل شعاع بسيط في كلتا الحالتين بحمل بسيط (قوة مركزة واحدة P1و P2).

الشكل 47
أ) الحالة الأولى للنظام (تحت الحمل P1);
ب) الحالة الثانية للنظام (تحت الحمل R2).
Δ 11 - الحركة في اتجاه الحمولة P1 P1.
Δ 21 - الحركة في اتجاه الحمولة R2في مكان تطبيقه من العمل P1.
Δ 22 - الحركة في اتجاه الحمولة R2في مكان تطبيقه من العمل R2.
- الحركة في اتجاه الحمولة P1في مكان تطبيقه من العمل R2.
تسمى الحركات ∆ 11 إلى ∆ 22 رئيسية ، وتسمى الحركات ∆ 12 إلى ∆ 21 ثانوية.
نظرية: إن عمل القوى الخارجية للحالة الأولى على النزوح الذي تسببه قوى الحالة الثانية يساوي عمل القوى الخارجية للحالة الثانية على النزوح الذي تسببه قوى الدولة الأولى.
دليل.
1) استخدم القوة أولاً P1 ،ثم تطبيق قوة على الحزمة المشوهة R2.
دعونا نحسب العمل الذي تقوم به القوى الخارجية (مع الانتباه إلى الشكل 48).
العمل المنجز بواسطة قوة مطبقة بشكل ثابت P1على إزاحتها الخاصة Δ 11 ، الناتجة عن هذه القوة ، سيتم تحديدها من التعبير:
العمل المنجز بواسطة قوة مطبقة بشكل ثابت R2على إزاحتها الخاصة Δ 22 سيتم تحديدها من تعبير مماثل:
 |
الشكل 48
في هذه الحالة ، العمل الإضافي للقوة المطبقة باستمرار بالفعل P1على الإزاحة Δ 12 التي تسببها القوة R2تحدد من التعبير:
(الانتباه إلى حقيقة أن العامل 1/2 غائب في التعبير ، منذ القوة P1ثابت عند الإزاحة Δ 12).
إجمالي عمل القوى الخارجية في ظل التسلسل المدروس لتطبيق الأحمال:
![]() .
.
2) الآن قم بتطبيق القوة أولاً R2، ثم نطبق القوة على النظام المشوه P1.
نحن نجادل بالمثل في الحالة الأولى. العمل بالقوة R2عند الإزاحة الذاتية 22 الناتجة عن هذه القوة:
العمل بالقوة P1عند الإزاحة الخاصة Δ 11:
قوة عمل إضافية P2على الإزاحة Δ 21 التي تسببها القوة P1:
(المضاعف 1/2 مفقود لأن القوة P2ثابت عند الإزاحة Δ 21).
ثم إجمالي عمل القوى الخارجية في ظل التسلسل المدروس لتطبيق الأحمال:
![]() .
.
بما أن عمل القوات لا يعتمد على ترتيب تطبيقها ، لذلك:
او غير ذلك:
وللحالة قيد النظر ؛
![]() .
.
بافتراض أن القوات المطبقة هي وحدة ف 1 =P2 = 1نحصل على المساواة في عمليات النزوح التي تسببها قوات الوحدة:
تثبت المساواة الأخيرة نظرية المعاملة بالمثل لعمليات النزوح:
إن إزاحة نقطة تطبيق قوة الوحدة في اتجاهها ، والناجمة عن قوة الوحدة الثانية ، تساوي إزاحة نقطة تطبيق قوة الوحدة الثانية في اتجاه الأخير ، الناتج عن فعل قوة الوحدة الأولى.
وبالمثل ، يمكننا إثبات المعاملة بالمثل للعمل الإضافي للقوى الداخلية:
للقيام بذلك ، ضع في اعتبارك عنصر شعاع بطول دز(الشكل 49).

 قاعدة لحساب احتمال وقوع حدث
قاعدة لحساب احتمال وقوع حدث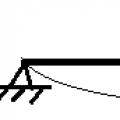 نظرية ماكسويل (نظرية المعاملة بالمثل لإزاحة الوحدات)
نظرية ماكسويل (نظرية المعاملة بالمثل لإزاحة الوحدات) صيغة قاعدة المصفوفة. تعلم البرمجة. مثال على قاعدة غير المشغل
صيغة قاعدة المصفوفة. تعلم البرمجة. مثال على قاعدة غير المشغل